The local average 
over the squared matrix elements
between states with E,N and E',N' then is
where the partial densities of states are defined in
eq. (2.36). Hence, the average is defined with the delta
functions of the energies as weighting factors. However, in the
present context 
is to be understood not as the Dirac
distribution but rather as a peaked function of suitable width. The
``suitable width'' is large compared to the average level spacing and
small compared to intervals over which secular variations of the level
densities occur. This guarantees that densities of states and strength
functions are smooth and can be reasonably approximated by the
expressions of subsection iiD. The strength produced by the
interaction operator 
is by specialization of eq. (3.1) and use of
eq. (2.30):
Note that of the seven quantities that specify the strength only six
are independent since t=p+a. Furthermore we observe that a nonzero
contribution comes only from the subspaces with 
and 
, because otherwise the matrix element vanishes. We proceed
to estimate this expression in three steps.
(i) In the first step the K-body matrix elements of 
are
considered to be entries of a random matrix. Invoking time reversal
invariance we postulate that (in K-body space) belongs to
the Gaussian orthogonal ensemble (GOE). This means that the second
moments of the matrix elements in eq. (2.27) can be expressed
by a single parameter 
, namely (a bar over a symbol denotes the
ensemble average)
for K-body configurations 
. Here,
is a generalized Kronecker symbol [19] with the
properties
This allows us to estimate the strength function (3.3) by
its ensemble average, or -- by the same token -- the spectral
average is identified with the ensemble average.
(ii) How does the correlation rule (3.4) translate into
the exciton picture? We find the following relation:
In principle, eq. (3.6) allows the simplification of the
various terms in the strength function (3.1). The evaluation
of the sum over the hole indices 
in eq. (3.3), however, is
complicated by the fact that it is not completely restricted in the
sense of eq. (2.22). We therefore use an approximation to
eq. (3.6):
The quality of this approximation is discussed in
appendix A, where the additional correlations resulting
from eq. (3.6) are found to be negligible. Note that
rule (3.7) implies that different exciton operators are
uncorrelated. Therefore the cross terms appearing in (3.1) do
not contribute to the strength function, which may consequently be
obtained by summing eq. (3.3) over k,a and q. With the
approximate correlation rule one easily arrives at:
The contribution of the second term on the r.h.s. of eq. (3.7)
is restricted to the diagonal elements of the matrix and is therefore
neglected relative to the first one. By eq. (3.8) the
problem factors into two aspects: All information that is specific for
the interaction is contained in . In the present paper this
factor is taken for granted. The remaining sum is common to all
interactions of body rank K. It represents the phase space aspect of
the problem, the propagation of the K-body force into the A-body
space.
The summation over 
, which appears for all operators
with k<K is now trivial and yields the factor 
.
(iii) The sum over 
is rewritten in a form which one can
call the separation of actors and spectators. The configurations
and 
that appear in the operators 
are called actors. They must appear in 
and 
, respectively, if the matrix element in
eq. (3.8) is to be different from zero. The remaining
configurations that are possibly present in and are called spectators. As proven in
appendix B one finds
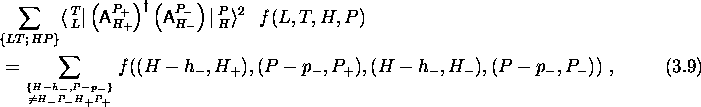
where f is any function that is completely symmetric in the indices
contained in L,T,H and P (for each group separately). The sum on
the r.h.s. of eq. (3.9) runs over the spectators. The
notation 
means a string of 
indices of holes
and a string of 
indices of particles that observe the
restrictions of eq. (2.22). In eq. (3.9), there is
the additional restriction 
which means that
none of the indices in is allowed to coincide with
any one of the indices in 
. By help of
eq. (3.9) one can simplify eq. (3.8) as follows
where we have used 
. As already mentioned, the sum over the spectators is not
independent of the sum over the actors: The spectators are not allowed
to occupy the exciton states of the actors. This is only a weak
condition if the dimensions of the single particle and single hole
spaces are much larger than the number of excitons that occur. If the
energies E and E' are not too high, this will be true and one can
treat the sums in eq. (3.10) as independent. This is called
the dilute gas approximation (DGA). It allows us to express the
strength function by the convolution of partial densities of states
As discussed in detail in appendix A, the conditions for
the validity of the DGA and for the applicability of the approximate
correlation rule (3.7) are essentially the same.