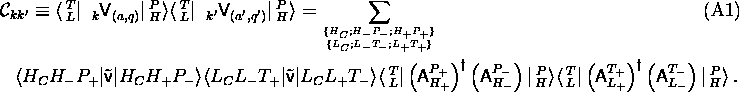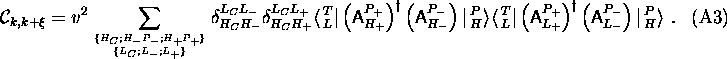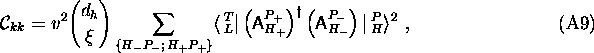In this appendix, the differences between the exact (3.6) and approximate (3.7) ensemble average are discussed. We find that eq. (3.6) leads to two types of additional correlation that do not appear in its approximation. Considering two examples, it will also be found, however, that these additional terms are of the same order of magnitude as those neglected by invoking the dilute gas approximation. Since the central formulae of section iiiA and iiiB rely on the DGA, it is not necessary and indeed would be inconsistent to take these quantities into account in the evaluation of the strength function.
The correlation coefficient for two operators is
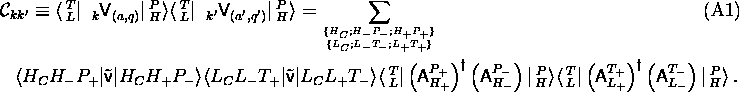
Estimating this expression by its ensemble average, we obtain:
Since hole and particle configurations by definition do not
intersect, the Kronecker symbol implies 
and 
.
Addition and subtraction of these equations yields q=q' and
a=a'. In other words: two operators that differ only
by their rank are correlated. This is the first difference to the ensemble
average (3.7) used in section iiiA, were it was found that
different operators are uncorrelated. The second type of additional
correlation we find in eq. (A2) results from the intricate
restriction pattern in the sum over hole configurations: The
restriction only applies to the indices within the groups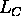 
and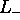 
. The condition for nonzero correlations, however, is that
the set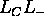 
of 
indices coincide with the set 
of 
indices. We adress these two cases one after the other.
First, let k' be equal to
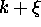with 
. The sum over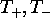 
may now readily be
carried out:
This expression may be simplified rather easily if we consider the
special case of 
. Then 
and we obtain
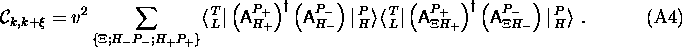
For further simplification of this expression let us introduce the
product of hole number operators
for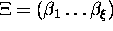 
. This operator has the property
where a term containing the factorial of a negative number is
understood to be zero. Note that
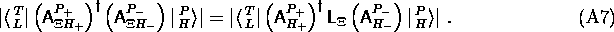
One therefore obtains
The quantity 
is the number of hole spectators,
cf. section iiiA. For the correlation coefficient of an operator
with itself, we find
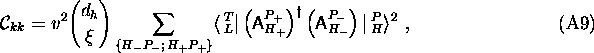
so that
Under the assumption that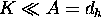 
, which implies 
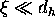, this yields
This type of correlation may therefore be neglected if the number of
spectators (in hole space) is small compared to the dimension 
of
the single hole space. This is certainly true if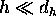 
, which
is the condition for the DGA introduced in section iiiA.
The second type of additional correlation appearing in eq. (A2)
shall be illustrated using the operator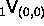 
of a two body interaction
(cf. Tab. I). We find for its correlation coefficient:
In the brackets, the first term is of the type discussed in
sections iiiA and iiiB. The second term is suppressed relative
to the first one by a factor 
and by the fact that it
contributes only to diagonal elements. The third term is suppressed
by a factor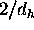 
. Obviously, it is justified to neglect the second
and third term as long as the DGA makes sense. Since out of the nine
operators of a two-body interaction which actually contribute to the
strength function 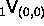is the only one that shows correlations of
this type, eq. (3.7) seems to be a very good approximation.