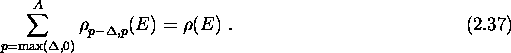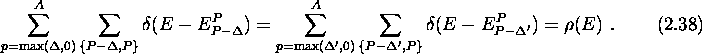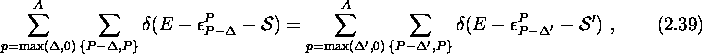In the statistical model of CN processes, reaction rates are dominated by the available phase space. This calls for a detailed knowledge of the densities of states, which have been the subject of intensive studies, see for example [11, 12, 13, 14]. In the present section, we quote the results relevant for the sequel. The density of states for the A-body system,
is approximated by continuous expressions derived with methods of
statistical mechanics. The famous Bethe formula is
Here, E is the excitation energy of the system,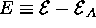 
(with the ground state energy 
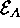) and g
is the single body density at the Fermi edge. Blatt and
Weisskopf [15] give the expression
which may be understood as an approximation to eq. (2.32)
in so far as it contains only the term varying most rapidly with energy.
Finally the approximation of constant temperature (CTA) yields a
purely exponential increase for the nuclear level density, i.e.
Here we have called the excitation energy y, because we will need the
total level density in this form in section ivB. The nuclear
temperature is defined as
Gilbert and Cameron [12] and v. Egidy and collaborators [16] have compared these expressions with experimental data on nuclear level densities and found that the CTA gives a good fit up to excitation energies of approximately 10 MeV, whereas above this value the Bethe or Blatt and Weisskopf expressions must be used.
Since we are going to work with the exciton picture, we need expressions for the densities of states with fixed exciton number. They will be characterized by the number of holes and particles that occur:
Here,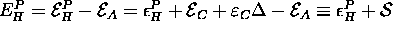 
. The
shift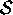 
is nonzero only if 
.
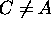Summation over the subspaces yields the total density of states:
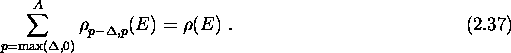
The identity (2.37) is of course independent of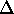 
. A
different 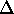merely implies a different description, but does
not alter the physics of the level density of the A-body system:
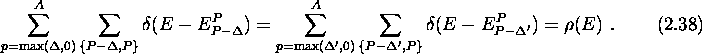
Since we are going to make use of this invariance property of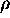 
in section iiiB, it is necessary to explain in detail how it is to
be understood. The sum over p on the r.h.s. of eq. (2.38)
may contain subspaces (e.g. 1p 3h
configurations) that do not appear at all on the left hand side (which
could start with the subspace of 2p 0h
configurations). And also the single exciton spaces are different: an
increase of decreases the dimension of the single hole space
and enlarges that of the single particle space. If we assume a
constant spacing of the single body levels, however,
the single exciton energies 
and 
in eqs. (2.17) and (2.18) that occur in the summations
over the subspace configurations are not affected by the
transformation (2.38) -- except for the highest
excited states. We can safely ignore this difference in the
energy range of interest. Explicitly, the identity (2.38)
then reads
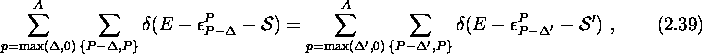
where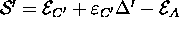 
, see below eq. (2.36).
Ericson [11] gave the
well-known approximate expression
for the partial density of states (2.36). It is valid if the
Pauli principle for excitons is ignored. This corresponds to the
``dilute gas approximation'' discussed below. Eq. (2.40) was
lateron improved in many respects (e.g. [17, 18]), but is
widely used because of its simplicity.