The spectral average over the squared matrix elements of 
implies sums over the basis states (2.15). To avoid double
counting of the basis states a definite order of the indices r and
in eq. (2.15) must be observed. We therefore introduce
the notation
Here, the 
with 
run over the
configurations 
. The sum is called restricted
because of the restriction 
imposed on the
permitted terms. Hence, the sum has 
terms.
In contrast the sum
is called unrestricted and has 
terms. Corresponding
conventions are used for the set P of particle configurations.
For later purposes we compress the notation of (2.22) further:
which means that the ordering has to be observed only within each
group of indices separated by semicolons.
In the following use will be made of the identity
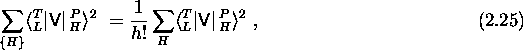
which holds because the squared matrix element is completely
symmetric with respect to the h indices in H, but vanishes if any
two of them coincide.