Propagation into the A-body space

 

In section iiiA, the matrix element was averaged over configurations with given exciton numbers. This result is useful if pre-equilibrium reactions are studied. In equilibrium CN reactions one asks for the average over the full A-body space which is defined as

 
in close analogy with eqs. (3.1) and (3.2). The summation of the partial strengths up to p,t=A is formally correct although in the energy range we are interested in (and committed to because of the DGA) by far not all subspaces come into play. The high energy subspaces are excluded by the multiplication with -functions. As discussed in the last section and in appendix A, different exciton operators are uncorrelated in the framework of the DGA. We therefore obtain the strength S(E',E) as a sum of the contributions by the operators :

 
in obvious notation. These contributions, in turn, are easily expressed by the strength functions (3.3):

 
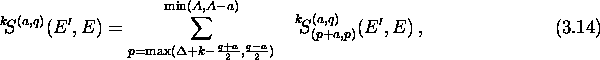
where the condition t=p+a has been used to evaluate one of the sums over the subspaces. The lower limit of the remaining sum guarantees that , (see below eq. (3.3)) and (see eq. (2.20)). The upper limit ensures that . We introduce the index of summation and the strength becomes:
 
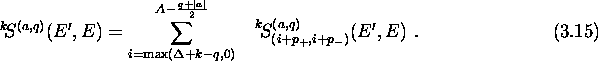
The second form of eq. (3.10) then yields
 
Here, the partial level densities of actors are the same as those in eq. (3.11). In eq. (3.16) the expression
 
appears with and . We want to compare R with the total density of states of the A-body system, the definition (2.37) of which is quite similar to the expression (3.17). The comparison with is possible if we exploit the invariance of the nuclear level density under shifts of the exciton vacuum. We recall eq. (2.39):

 
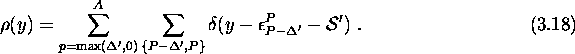
Expressions (3.18) and (3.17) differ in two respects :

1. The subspaces with do not appear in eq. (3.17).
2. The argument is shifted by .

In the energy range of typical CN reactions the first point is irrelevant so that the only remaining difference is the shift of the argument:
 
In the approximation of equidistant single body levels we find the relation:
 
At first sight one may be surprised to find that this relation depends on , which a priori we may choose arbitrarily. On the other hand, however, the choice of determines the quality of the DGA: it is best if those subspaces that contribute most to the strength are made up of as few excitons as possible. The more states are excluded by the Pauli-principle, the larger is the error in eq. (3.16). Evaluating the integral, we choose , which optimizes the DGA. Hence,

 
with
 
which is the energy needed to create z particles (negative z corresponds to the creation of holes).