Formula (3.21) can be evaluated by inserting Ericson's
expressions for the partial and the CTA for the total density of
states, see eqs. (2.40) and (2.34) . The operator 
then yields
the strength:
We have chosen 
in eq. (2.34). As mentioned in
section iiD, below 
MeV one should use the
temperature T tabulated in ref. [16]. For E>10 MeV, the
temperature should be determined from eq. (2.35), again with
[27]. In experiment, of course, the effect of the
interaction 
as a whole is measured. The spreading
width (2.1) is obtained by summing eq. (4.5)
over k,a and q after dividing through 
. This gives:
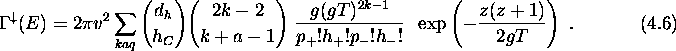
Usually a two-body ansatz is made for the interactions between
nucleons. We therefore explicitly carry out the summation in
eq. (4.6) for this case. The factor exp(-z(z+1)/2gT) by
which the total spectator density deviates from the nuclear level
density -- close to unity for typical values of T,g and E -- is
ignored here in order to analyze the general properties of the
spreading width. One finds:
which is a remarkably simple result. We emphasize two aspects of it:
(i) According to ref. [16] this is a constant as a function of
E below MeV because the nuclear temperature should
then be independent of E. At higher energy the leading term behaves
as 
. Altogether this amounts to quite a weak energy
dependence of 
for moderate E -- especially if
compared to the exponential energy dependence of 
. This result
is in qualitative agreement with the systematics of the spreading
widths pertaining to isospin violation [2]. Eq. (4.6)
shows that the leading energy dependence of will
be 
if the body rank of is K instead of
two. This demonstrates that the reason for the weak energy dependence
of the experimental is the two-body character of
the symmetry breaking interaction: With increasing excitation energy
the complexity (in terms of excitons) of the states increases. This
decreases the fraction of states that can be connected by an
interaction of low rank, hence the local average square 
decreases. Consequently, the product of and
varies slowly.
(ii) The contributions 
of the exciton
potential (k=1) and the exciton scattering (k=2) to the spreading
width are given by the first and second term on the r.h.s. of
eq. (4.7), i. e. by the terms proprotional to T and 
respectively. Inserting the typical value of T=0.5 MeV for
MeV [16] and 
as well as 
(which optimizes the DGA), one finds
Thus the rank one and rank two exciton interactions contribute about
equally strongly to in the energy range of
typical CN reactions.