The physical quantity we are interested in is the spreading width
Here, 
is the mean square matrix element of the
K-body interaction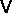 
, and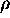 
is the level density of the
system. The matrix elements are calculated in a basis of eigenstates
to those parts of the Hamiltonian that dominate the behaviour of the
system. The spreading width due to additional, symmetry breaking
interactions then measures the extent of symmetry breaking in the
system. This may include the breaking of the independent particle
structure, isospin symmetry or parity by the residual strong, the
electromagnetic or weak interaction, respectively. In order to
properly treat the variation of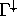 
with energy, the
average is limited to states in the neighbourhood
of some given excitation energy E. In fact, part of the present work
will consist of the calculation of the strength function
which implies the average over squared matrix elements between
configurations close to E and configurations close to E'. Once the
basis has been specified in detail, this local average will be
defined in section iii . The basis we work with is built up
from the single particle states 
that satisfy the
canonical Hartree-Fock equations
Here, D is the dimension of the one-body space spanned by the
discrete set of bound states, 
is the one-body kinetic energy
operator, and 
is the Hartree-Fock mean field
operator constructed from the strong nucleon-nucleon interaction,
which does not include the symmetry breaking interaction 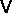for
which the spreading width shall be calculated. Let us introduce the
creation operators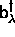 
and the physical
vacuum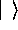 
so that
These operators fulfill the fundamental
anticommutation relation
A
basis of A-body states is then given by all possible A-fold
applications of creation operators:
with the condition
The energy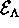 
of this many-body state is
The energy of the ground state 
is 
and will be denoted 
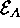. The
states (2.6) span the whole A-body space of dimension
, but for low energy considerations it is convenient
to split the A-body space into subspaces of increasing complexity
and energy and to restrict the description of the system to the
subspaces in the energy range of interest. Technically this idea is
realized by the transition to the exciton picture. For moderate
excitation energies the state of the system does not strongly differ
from the ground state and there will be only a few states occupied
above and unoccupied below the Fermi energy 
.
This will make it possible -- in
section iiiA -- to introduce the so-called dilute gas
approximation and treat the present problem in closed form.
Let us therefore introduce the exciton creation
operators [5, 6, 7] 
according
to [8]
acting on the exciton vacuum
One then has 
for all 
and
the anticommutation relation (2.5) holds for the operators 
, too. Briefly: the excitons are fermions. The single body space is
split into two subspaces, the single particle space with dimension
and the single hole space with dimension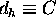 
. The exciton vacuum 
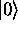-- the core -- need not be
identical to the ground state of the A-body system under
consideration, i.e. at present we do not fix
The energy of the vacuum is called
Every configuration 
can then be characterized by a
vector
of its particle configurations and by a vector
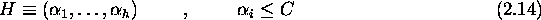
of
its hole configurations. Every independent particle configuration
can be expressed in the form
The combination of operators
appearing in this equation will also be written as
As usual we introduce the energies
of the particle configurations relative to the core level as well as
the energies of the hole configurations
The energy of the state (2.15) then is
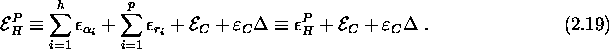
The symbol 
has been introduced to simplify the
notation. In the present paper the letters r,s,t,u or v
will be used for particle states and 
or
for hole states; configurations of the physical
constituents of the system -- called bodies -- are labelled
or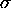 
. If one chooses C<A, the
ground state of the system has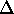 
particles and no holes,
otherwise it has no particles and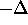 
holes. Generally one has
The maximum number of particles is A and that of holes
. Hence, the exciton picture provides a decomposition of
the A-body space into mutually orthogonal subspaces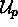 
,
. The dimension of the subspace 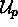is 
. We use the
following notation for many-exciton states: A state 
contains the same numbers of particles and holes as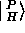 
on possibly different single exciton states. A ket
on the other hand differs from 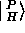with respect to exciton number as well as single exciton
states.
