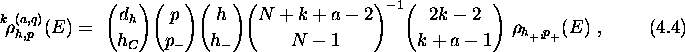Transition rates in the exciton model

  Formula (3.11) can be applied to the exciton model of preequilibrium nuclear reactions. In this model, which was formulated by Griffin [20] and has later been refined by several authors [21, 22, 23, 24], an important concept is that of transition rates between subspaces of different exciton number. These appear in the Master equation for the time dependence of the system. Transitions are assumed to be caused by the residual interaction of a strong two-body force 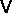. The rate for going from the subspace 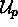to 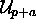is given by
 
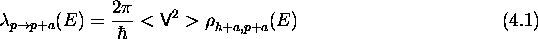
and is related to the strength calculated in section iiiA according to
 
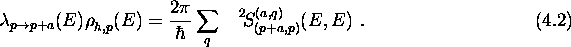
Note that the residual interaction consists by definition of the operators with exciton rank k=2 that appear if 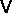is expressed in the exciton picture using the Hartree-Fock single exciton configurations. Invoking the Ericson densities (2.40) and , the convolution (3.11) can easily be evaluated and leads to the transition rate
 
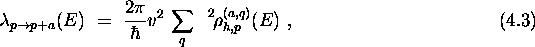
with the density of final states
 
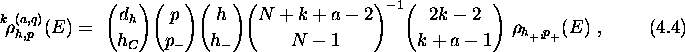
where N=p+h, see above eq. (3.1). Because of the last binomial only operators with k>|a| contribute. The final state densities that appear here in the context of propagation of the defining GOE matrix elements have been obtained earlier for k=2 by combinatorial arguments on the states accessible in two-body collisions [25, 26, 18]. Originally, 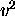was a fit parameter. It is identified here as the average square of the antisymmetric K-body matrix element.