M. Granzow, H. Riedel, and B. Kollmeier
FB 8, AG Medizinische Physik
Carl-von-Ossietzky-Universität Oldenburg, Germany
One of the major experimental obstacles to unambiguous interpretation of early auditory evoked potentials is the usually poor signal-to-noise ratio of the averaged data. For responses to stimuli well above threshold Mühler and von Specht [Audiologische Akustik, 35:12-20 (1996)] recently suggested a technique to reduce the noise contamination: The recorded single sweeps are processed with a finite impulse response filter and the inverse of the variance of the resulting signal is used as its weight in the average.
In the present study the extent to which this procedure can improve the quality of 32-channel recordings of early auditory evoked potentials is investigated. Several quantitative estimates of the quality of the resulting average are considered and their dependence on the cutoff frequency of the finite impulse response filters and on the type of weighting factor is established.
INTRODUCTION
If one tries to improve the quality of EEG measurements - early evoked potentials in particular - the most straightforward approach is to increase the number of epochs that enter the average. Assuming the noise to be uncorrelated from epoch to epoch, this procedure doubles the signal-to-noise ratio every time the number of epochs is quadrupled. Obviously, increasing epoch number becomes relatively ineffective as soon as the number of epochs is about 103. The use of several thousand sweeps is, however, common practice in the recording of early auditory evoked potentials. It is therefore necessary to develop different strategies, e. g., frequency selective filtering. Given the time scale of action potentials (1 ms), all frequencies above 2000 Hz are usually discarded. Since much of the remaining noise is generally assumed to be located at low frequencies (zero to a few hundred Hz), it has been suggested to highpass filter the single sweeps prior to weighted averaging [1]. Steep infinite impulse response filters, however, tend to produce deleterious deformations of the waveforms because of their nonlinear phase response. Therefore finite impulse response (fir) filters designed to have linear phase have been used in the present study to reduce the noise contamination of auditory evoked EEG-epochs.
DATA ACQUISITION
Two sets of ten thousand responses of a
normal hearing subject to monaural
stimulation of the left and the right ear at
60 dB (SL) were recorded from 32 electrodes
on the scalp. Stimuli were 100 
s clicks
presented by means of insert earphones.
Measurements were performed in an
electrically and acoustically shielded
chamber. During recording, only an analog
anti-aliasing filter was employed. Artifact
threshold was chosen non-restrictively and
set to a high value, avoiding only clipping
of the analog-to-digital converters.
DATA PROCESSING
The epochs were filtered offline with finite
impulse response bandpass filters of
order 144, lower cutoff frequencies 0, 50,
100, 
, 300 Hz, and fixed upper
cutoff frequency of 2000 Hz. The transfer functions
are shown in Fig. 1. The phase
responses of the filters are exactly linear.
The lower cutoff frequency of 0 Hz corresponds to a
pure lowpass filter.
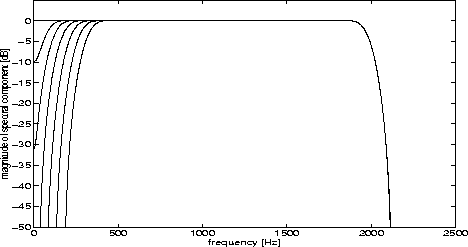
Figure 1: Transfer functions of the fir
filters used in this study.
Filter order and recording interval
were tailored to leave 10 ms of usable
data. Prior to filtering the voltage of the
first sample in each channel was subtracted
from all samples of that channel to make sure
the step response of the filter did not
contaminate the data. From the epochs thus
obtained, various averages were computed. An
artifact threshold of 5, 6, , 20
V was imposed to exclude epochs that
showed peak-to-peak voltages above twice
those values. The remaining epochs were then
weighted either with the inverse of their variance,
or with the inverse of their
root-mean-square value, or not weighted at
all, yielding forty-eight different averages
for each filter condition.
MEASURES OF DATA QUALITY
It is principally impossible to determine
the signal-to-noise ratio (SNR) of
experimentally obtained data. However, the
most plausible definition of the
residual noise rn (t) of a
measurement is the standard deviation of the
average:
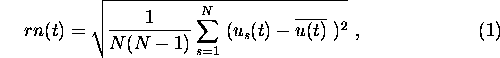
N being the number of sweeps entering the
average, 
the voltage in sweep s
at time sample t, and 
the
average across sweeps. For weighted averages
the corresponding formula is
with the weighting factor 
and the
normalisation coefficient 
. Obviously, eq. (1) corresponds
to eq. (2) with 
for
all s. Dividing the rms value of the
average by the rms value of rn (t) one
obtains a single sweep based estimate of the
SNR, which we will call s:
where T is the number of time points per
sweep. Since the evaluation of 
is computationally very costly, two average
based SNR-estimates are frequently employed:
One approach is to add and subtract two averaged
responses 
and
to the same
stimulus. One then defines the estimate
q as follows:
Here, the sum is assumed to be the double of
the signal and the difference 
times the noise. The other estimate of data
quality is the correlation coefficient
r between
and 
.
RESULTS
The three columns of plots in Fig. 2 show the variation of these quantities (averaged across channels) with lower cutoff frequency and artifact threshold for no weighting, 1/rms-weighting and 1/variance-weighting, respectively, for the responses to the right ear (the responses to left-ear stimulation show a very similar behaviour). The first row displays s, the second q, and the third r, respectively.
The general tendency of a peak at a medium cutoff frequency and relative stability against the artifact threshold is the same for all three cases. In order to localize the maximum with respect to lower cutoff frequency, the region between 50 and 150 Hz has been resolved in steps of 10 Hz.
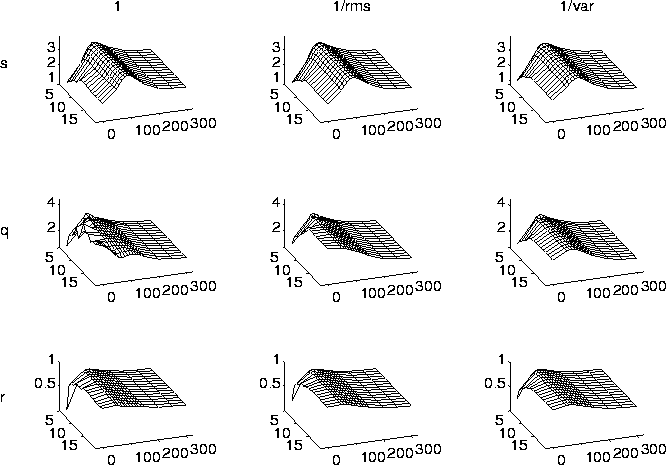
Figure 2: Measures of data
quality as functions of lower
cutoff frequency in Hz (to the
right) and artifact threshold
in 
V (to the front).
Note that the maxima of s are more pronounced than those of q and r, and furthermore occur at the same highpass cutoff frequency (90 Hz) irrespective of the weighting factor, whereas the location of the maxima of q and r is influenced by the weighting method.
PRINCIPAL COMPONENT ANALYSIS
A measure not of the quality, but of the extent to which a set of data is suited for a multi-parameter fit is the principal component analysis (PCA). The principal value associated with a principal vector of a measurement matrix indicates which fraction of the data can be explained by that principal vector. The number of principal vectors that have to be included to explain, say, 95 % of the data therefore indicates how many independent parameters can be fitted to the data. PCAs of the averages calculated as explained above have been carried out. Figures 3 and 4 show the number of principal components needed to explain 95 % of the 1/variance-weighted average, and which fraction of the same data can be explained by the cumulative inclusion of principal components for various lower cutoff frequencies.
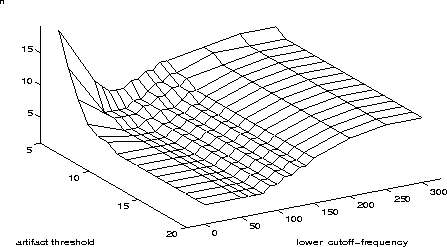
Figure 3: Number n of principal components
needed to explain 95 % of the
data.
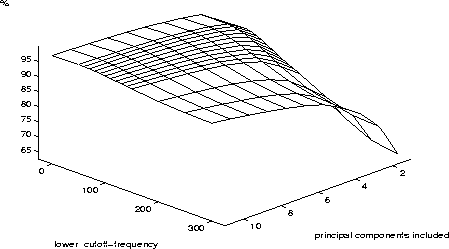
Figure 4: Fraction of data
in % explained by
the cumulative inclusion of
principal components.
Clearly, the variance is more evenly distributed among the principal components if the low frequency components are excluded from the average.
DISCUSSION
In the present study, the influence of the preprocessing of the single sweeps that make up an average on data quality, as reflected in various SNR measures, has been investigated. Estimates of the signal-to-noise ratio that are commonly used (q and r) as well as the computationally much more costly s have been considered. For all three measures the effect of weighting is found to be negligible except for the case of no high-pass-filtering at all, where it does smooth out fluctuations of the quality measures with artifact threshold. This finding is at variance with the manifest influence of weighting on data quality reported for some subjects in [1]. Since large variation of the noise from epoch to epoch is necessary for the weighting to be effective [2], this difference may be due to the fact that noise does not vary strongly between epochs for the data we have analysed.
Our results for s point to an
optimal highpass frequency of 90 Hz for early
auditory evoked potentials in contrast to
about 60 Hz if the conventional
signal-to-noise ratio estimates 
or 
are used. It should be
emphasized that such a choice applies only
to adult subjects hearing clicks well above
threshold. Sininger [3] found
the quality of averaged responses from
neonates to tone bursts to be higher with a
lower cutoff frequency of 30 Hz than with one
of 150 Hz.
We regard s as the most reliable SNR estimate because it shows only a global maximum with respect to lower cutoff frequency which does not vary significantly with weighting mode and artifact threshold.
The sharp increase in the number of important principal components with lower cutoff frequency indicates that much of the variance is in fact contained in the low frequency domain. Only five principal components are needed, however, to explain most of the variance of the average with the highest s. It does therefore not seem to be possible to extract more information from our data than a handful of independent parameters, corresponding to a fit with at most two dipoles (three parameters each). This appears to be an important limitation for the analysis of the current data.
It should be noted, however, that the present findings need further support by an analysis of data from more subjects with the same methods.
